永遠の初心者を脱却するには
独学の開始
初めてのナレッジ投稿になります。pythonを始める動機は人それぞれですが、個人的な印象では、スクレイピング、A I、機械学習、業務効率化が多いような気がします。私の場合は、漠然とDeep learningをしたいというのが動機の一つでした。言語仕様が比較的シンプルと言われていて、しかも数値計算に関わるパッケージが充実しているため、より直接的に数学的な処理が出来ると思いpythonを選択しました。こうして、テキストを買ってPythonの独学が始まりました。
永遠の初心者という不安
しかしながら、慣れ親しんでいた言語と様子が違って見える事に戸惑い、最初に選んだテキストが難しく、自然とより簡単な本へと入門書を梯子する事になりました。その結果、サンプルプログラム等を通じて基礎力は付いたものの、なかなか自分で一から考えてプログラムを作ることができませんでした。職場での業務では経験したことの無い、得体の知れない不安が大きくなっていきました。無理やり言葉にするならば、このまま「永遠の初心者」のまま終わってしまうのではないか?となるかもしれません。
独学と業務はどう違うのか?
職場では多くの場合メンター的存在がいて、しかも一定量まとまったプログラムを半強制的に作るために、気づくと自動的に初心者を脱却していたのだと思いますが、自宅で独学していた私にはメンターも強制力もありませんでした。
転機
そんな私にも転機が訪れました。それは「有限個の微分不可能な点を許した連続関数の零点を、与えられた区間内で網羅的に求める」という問題意識を持ったことです。微分可能性を仮定して零点を求める手法はニュートン法を初め多くあります。私の問題意識は、僅かにその仮定を緩めたものですが、微分を使ってはいけないため、一から手法を編み出さなければなりませんでした。その重点ポイントを箇条書きすると、次のようになります。
1.大局的にどのあたりに零点がありそうか探査すること。
2.いつ、1の探査を止めて、局所的な探査に移行するか?
3.零点がありそうな場所で、局所的に精度よく零点を探査すること。
4.いつ、3の探査を止めるべきか?
下図は、実際に作成したPythonスクリプトで零点を求めた例です。
グラフは視覚的に零点候補の場所を示しているが、本アルゴリズムの要点ではない。
むしろ、sin(x)の零点である円周率(π=3.1415926535897932・・・)の値と比較するとかなり精度が高いことが分かる。
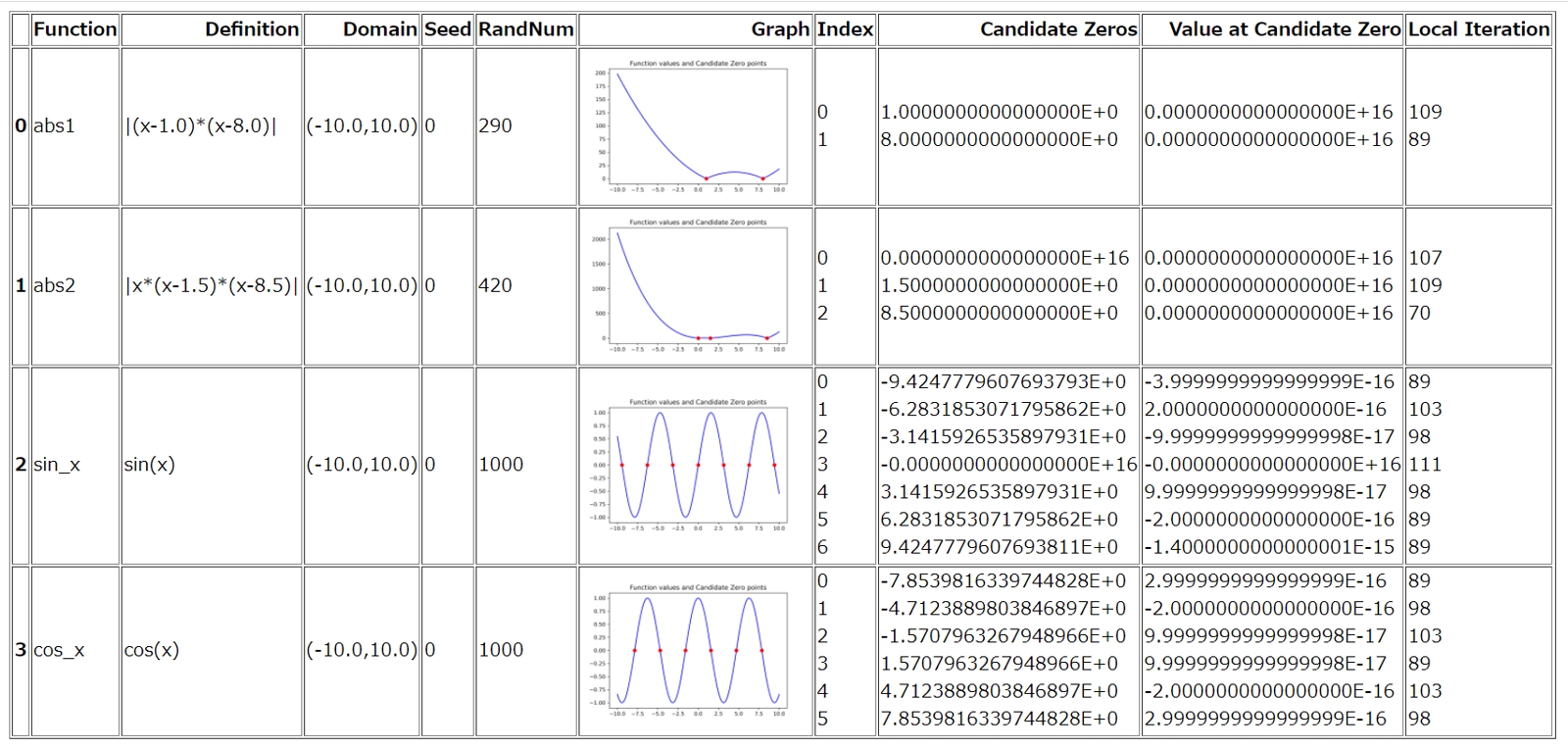
Definition:関数の定義式
Domain :定義域
Candidate Zeros :零点候補
Value at Candidate Zero :零点候補における関数値
何が変わったか?
さて、上のように問題意識を持ってアルゴリズム開発に取り組んだ結果、何が変わったか?別に誰か偉い人から認めてもらった訳でも、収入が増えた訳でもなく、自己満足の域を出ていないと思います。それでも、「永遠の初心者」の不安が消えてしまったのです。Pythonに関するスキルが特段向上した訳ではないと思いますが、「これで初心者から脱却できた!」と思えるようになりました。そして、それからはPythonプログラミングにおいて、様々起きるエラー等にも割と短時間で対処できるようになってきました。初心者の頃に量をもって学んだ基礎が質に変化したというべきでしょうか?
送る言葉
このような経験を踏まえて、今まさに「初心者の壁」に阻まれ悩んでいる方には、次の言葉を送りたいと思います。「自分が興味を持つテーマに対して、既存の枠組みを少しだけ拡張するために、Pythonを利用してみてください。」



